§0 準備編¶

§0.1 Julia のインストール¶

§0.1.1 Mac の場合¶

Homebrew (https://brew.sh/ja/) を利用する.

$ brew install --cask julia

§0.1.2 Windows or Linux の場合¶

https://qiita.com/ttabata/items/b05bb43d06239f968035 参照.

§0.2 JupyterLab のインストール¶

Anaconda で Python ごと丸っと入れるのがラク.　https://hituji-ws.com/code/python/python_env_ana/ 参照.

JupyterLab で Julia を使うには https://leadinge.co.jp/julialang/2022/04/06/jupyterlab/ 参照.

§0.3 パッケージを読み込む¶

In [78]:
# 初回だけで OK
import Pkg
Pkg.add("Plots")
Pkg.add("DifferentialEquations")
Pkg.add("Optim")
Pkg.add("Printf")
Pkg.add("ForwardDiff")
Pkg.add("QuadGK")
Pkg.add("Interpolations")
Pkg.add("LinearAlgebra")

   Resolving package versions...
  No Changes to `~/.julia/environments/v1.11/Project.toml`
  No Changes to `~/.julia/environments/v1.11/Manifest.toml`
   Resolving package versions...
  No Changes to `~/.julia/environments/v1.11/Project.toml`
  No Changes to `~/.julia/environments/v1.11/Manifest.toml`
   Resolving package versions...
  No Changes to `~/.julia/environments/v1.11/Project.toml`
  No Changes to `~/.julia/environments/v1.11/Manifest.toml`
   Resolving package versions...
  No Changes to `~/.julia/environments/v1.11/Project.toml`
  No Changes to `~/.julia/environments/v1.11/Manifest.toml`
   Resolving package versions...
  No Changes to `~/.julia/environments/v1.11/Project.toml`
  No Changes to `~/.julia/environments/v1.11/Manifest.toml`
   Resolving package versions...
  No Changes to `~/.julia/environments/v1.11/Project.toml`
  No Changes to `~/.julia/environments/v1.11/Manifest.toml`
   Resolving package versions...
  No Changes to `~/.julia/environments/v1.11/Project.toml`
  No Changes to `~/.julia/environments/v1.11/Manifest.toml`
   Resolving package versions...
  No Changes to `~/.julia/environments/v1.11/Project.toml`
  No Changes to `~/.julia/environments/v1.11/Manifest.toml`
In [32]:
# こっちは毎回
using Plots, DifferentialEquations, Optim, Printf, ForwardDiff, QuadGK, Interpolations, LinearAlgebra

§1 基本編¶

https://webpark1378.sakura.ne.jp/nagai/julianote.pdf 参照.

§1.1 練習問題¶

  1. $178 + 256$

  2. $\cos(\exp(3)) + \sin(\exp(4))$

  3. $ \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} \begin{pmatrix} 5 \\ 6 \end{pmatrix} $

  4. $A=\begin{pmatrix} 1 & 3 \\ 2 & 3 \end{pmatrix}$, $B=\begin{pmatrix} 4 & 7 \\ 9 & 5 \end{pmatrix}$ のとき $AB$ の $(1,2)$ 成分.

  5. $A=\begin{pmatrix} 2 & 3 \\ 4 & 5 \end{pmatrix}$ の各成分を $3$ 倍.

  6. $\sum_{i=1}^{100}\cos(i)$ を for 文と内包表記の 2 つの方法で求めよ.

  7. $\cos(x)$ をプロットせよ.

  8. 正の整数 $n$ に対し, それが偶数なら $n/2$ を, 奇数なら $3n+1$ を返す関数 $$f(x)=\begin{cases} n/2 & \text{for $n\equiv0$} \\ 3n+1 & \text{for $n\equiv1$} \end{cases} \quad\mod{2},$$ を定義せよ. 正の整数 $n$ に対し操作 $f$ を繰り返し, $1$ になるまでの結果を全て出力する関数 $\mathrm{Collatz}(n)$ を定義せよ.

解答¶

In [66]:
178+256
Out[66]:
434
In [68]:
cos(exp(3)) + sin(exp(4))
Out[68]:
-0.600173180811254
In [78]:
[1 2 
3 4]*[5 
6]
Out[78]:
2-element Vector{Int64}:
 17
 39
In [92]:
A = [1 3
2 3]
B = [4 7
9 5]
(A*B)[1,2]
Out[92]:
22
In [96]:
A = [2 3
4 5]
A .* 3
Out[96]:
2×2 Matrix{Int64}:
  6   9
 12  15
In [110]:
S = 0
for i in 1:100
    S += cos(i)
end
@show S

S = -0.5322886082303911
Out[110]:
-0.5322886082303911
In [114]:
sum([cos(i) for i in 1:100])
Out[114]:
-0.5322886082303911
In [18]:
plot(0:0.01:10, cos)
Out[18]:
In [174]:
function f(n) # コラッツ関数
    if !(isinteger(n) && n>0) # (整数かつ正) でなかったら
        return 1
    elseif iseven(n) # (整数かつ正) かつ偶数なら
        return div(n,2)
    else
        return 3n+1 # (整数かつ正) だけど偶数でなかったら
    end
end      

function Collatz(n)
    while n != 1
        n = f(n)
        @show n  
    end
end
Out[174]:
Collatz (generic function with 1 method)
In [176]:
f(4)
Out[176]:
2
In [212]:
Collatz(27)

n = 82
n = 41
n = 124
n = 62
n = 31
n = 94
n = 47
n = 142
n = 71
n = 214
n = 107
n = 322
n = 161
n = 484
n = 242
n = 121
n = 364
n = 182
n = 91
n = 274
n = 137
n = 412
n = 206
n = 103
n = 310
n = 155
n = 466
n = 233
n = 700
n = 350
n = 175
n = 526
n = 263
n = 790
n = 395
n = 1186
n = 593
n = 1780
n = 890
n = 445
n = 1336
n = 668
n = 334
n = 167
n = 502
n = 251
n = 754
n = 377
n = 1132
n = 566
n = 283
n = 850
n = 425
n = 1276
n = 638
n = 319
n = 958
n = 479
n = 1438
n = 719
n = 2158
n = 1079
n = 3238
n = 1619
n = 4858
n = 2429
n = 7288
n = 3644
n = 1822
n = 911
n = 2734
n = 1367
n = 4102
n = 2051
n = 6154
n = 3077
n = 9232
n = 4616
n = 2308
n = 1154
n = 577
n = 1732
n = 866
n = 433
n = 1300
n = 650
n = 325
n = 976
n = 488
n = 244
n = 122
n = 61
n = 184
n = 92
n = 46
n = 23
n = 70
n = 35
n = 106
n = 53
n = 160
n = 80
n = 40
n = 20
n = 10
n = 5
n = 16
n = 8
n = 4
n = 2
n = 1

§ 1.2 常微分方程式¶

常微分方程式 $$\frac{\mathrm{d}x(t)}{\mathrm{d}t}=x(t),$$ を解いてみよう. 微分して同形なので $$ x(t) = C\mathrm{e}^t, $$ だとわかる. $C$ は積分定数.

では $$\frac{\mathrm{d}x(t)}{\mathrm{d}t}=x^3(t)+1, \tag{1}$$ なら？

一般に常微分方程式 $$\frac{\mathrm{d}x(t)}{\mathrm{d}t}=f(x), \tag{2}$$ は解析的に解けるとは限らない. しかし $f(x)$ を評価できるなら以下のように数値的に概形を求めることはできる.

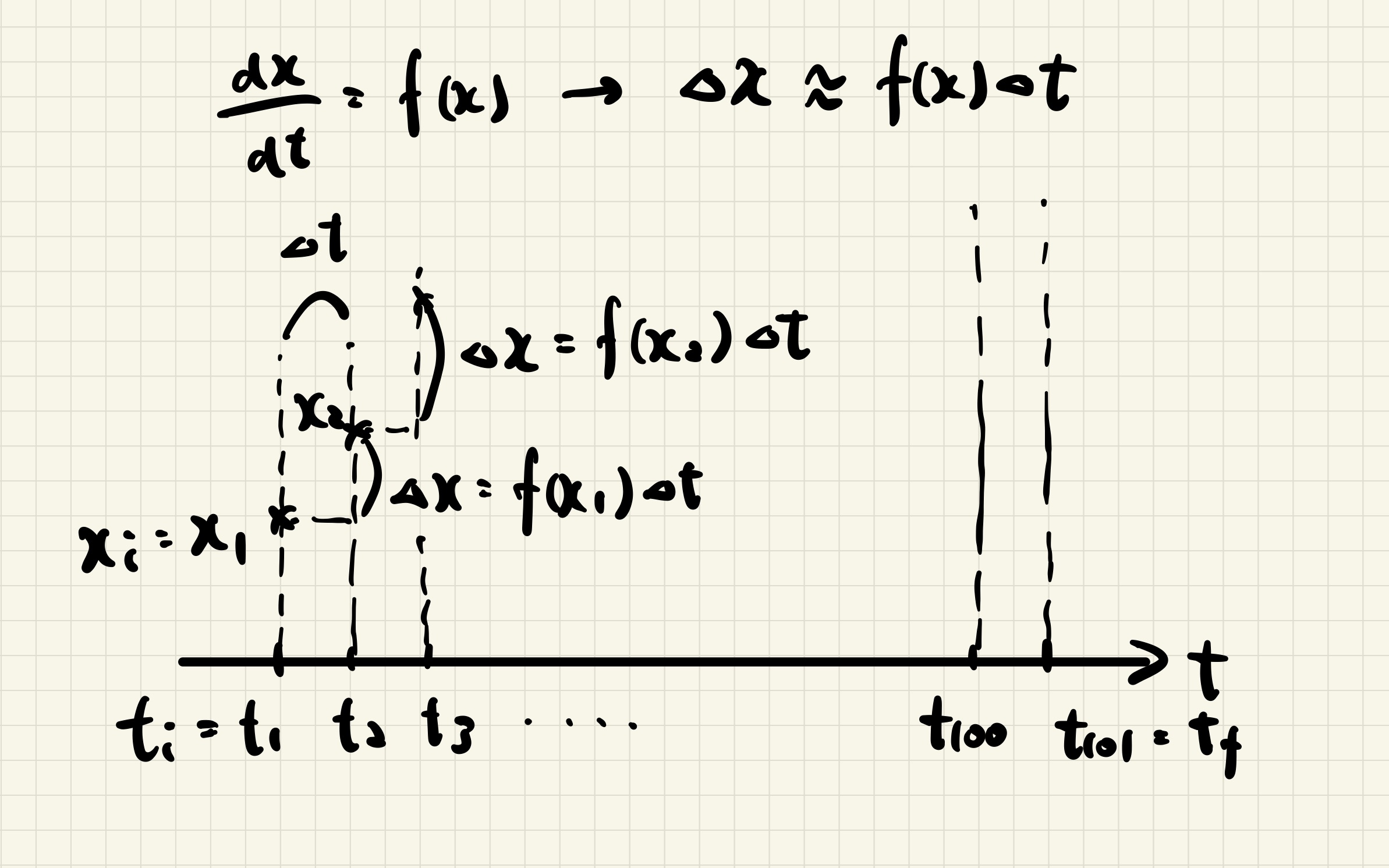No description has been provided for this image まず解きたい $t$ の範囲 $[t_\mathrm{i},t_\mathrm{f}]$ を適当に分割する (例えば $100$ 等分; $\Delta t=(t_\mathrm{f}-t_\mathrm{i})/100$). $x$ は初期時刻 $t_\mathrm{i}=t_1$ において $x_\mathrm{i}$ にいるとする. このとき次の時刻 $t_2=t_1+\Delta t$ に $x$ はどこにいるかを考えよう. 微分の定義より $\Delta t$ が十分小さければ以下の近似が成り立つ. $$\frac{x(t_2=t_1+\Delta t)-x(t_1)}{\Delta t}\approx\left.\frac{\mathrm{d}x(t)}{\mathrm{d}t}\right|_{t=t_1}=f(x_1).$$ したがって $x_2=x(t_2)=x(t_1+\Delta t)$ は $$x_2\approx x_1+f(x_1)\Delta t,$$ ともとまる. 同様に $x_3=x(t_3)$ は $$x_3\approx x_2+f(x_2)\Delta t,$$ だし $n$ 番目の位置 $x_n$ はその 1 つ前の位置 $x_{n-1}$ から $$x_n\approx x_{n-1}+f(x_{n-1})\Delta t, \tag{3} $$ ともとまる. これを繰り返せば好きな時刻 $t$ の $x$ が求められるので, 元の微分方程式 (2) が近似的に解けたと言えるだろう. このように差分近似を用いて微分方程式を数値的に解く手法を「数値解法」と言い, 特に (3) 式で近似することを「オイラー法」と呼ぶ (cf. 映画「ドリーム」 (原題: Hidden Figures)). オイラー法は数値解法の中で最も単純な方法であり, 現在までに様々な解法が提唱されている.

問題¶

オイラー法を用いて常微分方程式 (3) $$\frac{\mathrm{d}x(t)}{\mathrm{d}t}=x^3(t)+1,$$ を, 初期条件 $t_\mathrm{i}=0$, $x_\mathrm{i}=0$ のもとで数値的に解き, 結果をプロットせよ.

In [82]:
f(x) = x^3+1

# 解く時刻範囲 [ti, tf] と時刻幅 dt
ti = 0
tf = 1
N = 100
dt = (tf-ti)/N
tlist = ti:dt:tf

xlist = zeros(N+1) # 空の 101 要素配列を用意しておく.

xi = 0
xlist[1] = xi # xlist の最初の要素に初期条件 xi を代入.

for i in 1:N
    xlist[i+1] = xlist[i] + f(xlist[i])*dt # オイラー法
end

plot(tlist,xlist)
Out[82]:

§1.2.1 パッケージを使う¶

様々な数値解法が "DifferentialEquations" パッケージに用意されている.

In [92]:
ODE(x,p,t) = f(x) # p: パラメータ (あれば). 1 変数の場合はこの形で dx/dt を用意しておかなければならない
prob = ODEProblem(ODE, xi, (ti,tf)) # 微分方程式を定義
@time sol = solve(prob, Tsit5()); # Tsit5 (可変時間刻み Runge--Kutta) アルゴリズムで解く

  0.250389 seconds (670.31 k allocations: 37.314 MiB, 99.98% compilation time: 100% of which was recompilation)
In [94]:
plot(sol.t,sol.u,st=:scatter)
plot!(tlist,xlist) # オイラー法で計算した線と重ねる
Out[94]:
In [96]:
@time sol = solve(prob, Tsit5(); reltol=1e-10, abstol=1e-10); # 刻みが粗いので要求精度を上げる

  0.061396 seconds (207.80 k allocations: 14.739 MiB, 99.91% compilation time: 100% of which was recompilation)
In [98]:
plot(sol.t,sol.u,st=:scatter)
plot!(tlist,xlist) # オイラー法で計算した線と重ねる
Out[98]:

問題¶

微分方程式 $$\frac{\mathrm{d}x}{\mathrm{d}t}=x^3-x,$$ を初期条件 $x_{\mathrm{i},0}=1$, $x_{\mathrm{i},1}=1+10^{-5}$, $x_{\mathrm{i},2}=1-10^{-5}$ の 3 パターンで $t_\mathrm{i}=0$ から $t_\mathrm{f}=5$ まで解き, 重ねてプロットせよ.

In [20]:
Lorenz(x,p,t) = x^3-x 

ti = 0
tf = 5
xi0 = 1
xi1 = 1 + 1e-5
xi2 = 1 - 1e-5

prob0 = ODEProblem(Lorenz, xi0, (ti,tf)) 
prob1 = ODEProblem(Lorenz, xi1, (ti,tf)) 
prob2 = ODEProblem(Lorenz, xi2, (ti,tf)) 
@time sol0 = solve(prob0, Tsit5(); reltol=1e-10, abstol=1e-10) 
@time sol1 = solve(prob1, Tsit5(); reltol=1e-10, abstol=1e-10) 
@time sol2 = solve(prob2, Tsit5(); reltol=1e-10, abstol=1e-10) 

plot(sol0.t,sol0.u)
plot!(sol1.t,sol1.u)
plot!(sol2.t,sol2.u)

  0.371189 seconds (1.70 M allocations: 94.511 MiB, 99.94% compilation time)
  0.033806 seconds (207.46 k allocations: 11.278 MiB, 99.70% compilation time)
  0.000044 seconds (191 allocations: 16.125 KiB)
Out[20]:

§2 ニュートン力学¶

ニュートンの運動方程式 $$m\frac{\mathrm{d}^2x}{\mathrm{d}t^2}=F.$$ を解いてみよう. 2 階微分方程式を解くには, 位置 $x$ と速度 $v$ の 2 変数を用意して $$\begin{cases} \displaystyle \frac{\mathrm{d}x}{\mathrm{d}t}=v, \\[5pt] \displaystyle \frac{\mathrm{d}v}{\mathrm{d}t}=\frac{F}{m}. \end{cases}$$ と 2 連 1 階微分方程式にすればいい.

§2.1 単振動¶

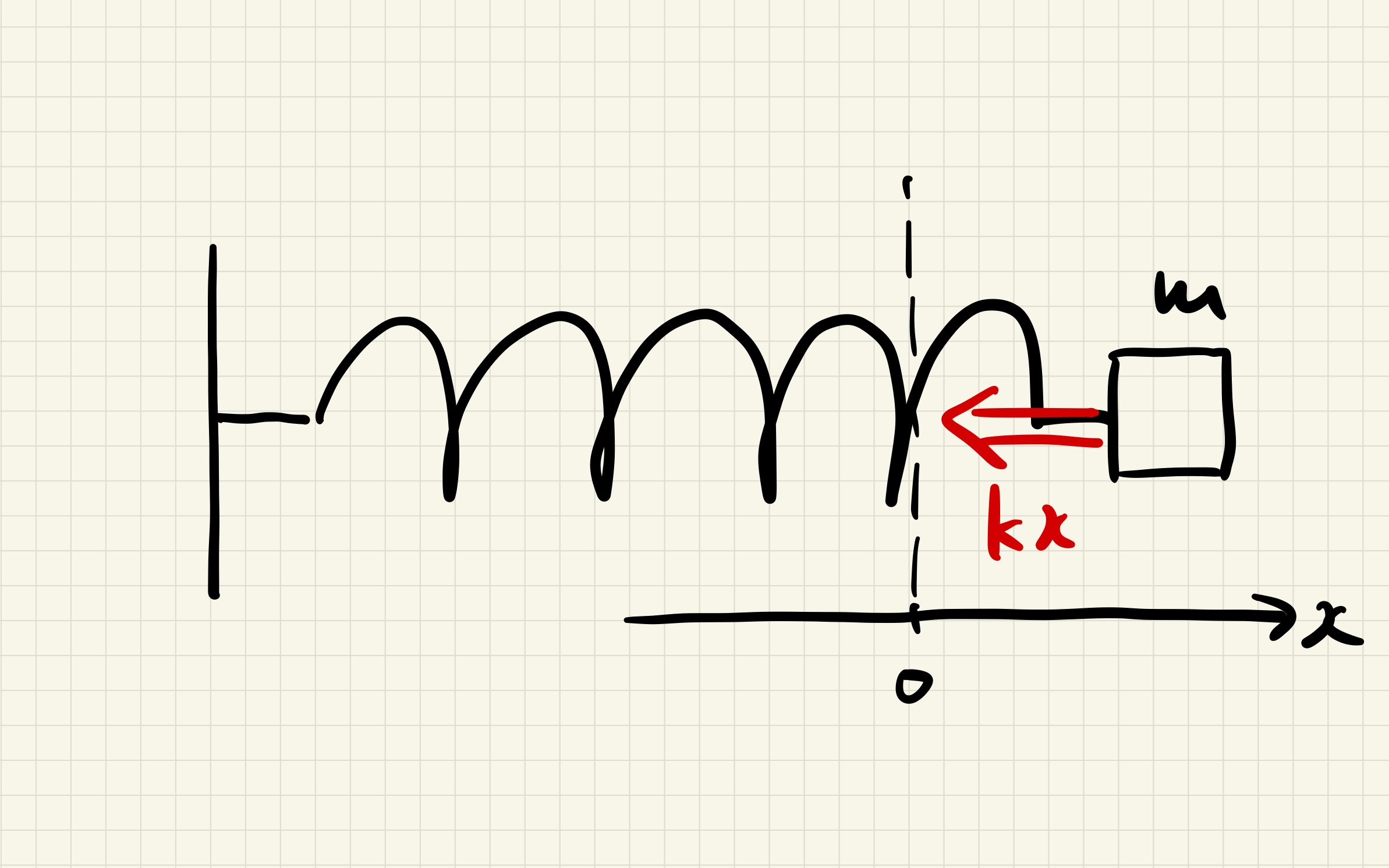No description has been provided for this image $$m\frac{\mathrm{d}^2x}{\mathrm{d}t^2}=-kx.$$ あるいは $$\begin{cases} \displaystyle \frac{\mathrm{d}x}{\mathrm{d}t}=v, \\[5pt] \displaystyle \frac{\mathrm{d}v}{\mathrm{d}t}=-\frac{k}{m}x. \end{cases}$$
In [100]:
# 微分 du, 変数 u, パラメータ p, 時間 t
# u[1] = x, u[2] = v
# p[1] = m, p[2] = k
function HarmonicOscillator(du, u, p, t)
    du[1] = u[2] # dx/dt = v
    du[2] = -p[2]/p[1]*u[1] # dv/dt = -k/m * x
end
Out[100]:
HarmonicOscillator (generic function with 1 method)
In [102]:
m = 1  # 質量
k = 1  # ばね定数
    
xi = 1  # x の初期値
vi = 0  # v の初期値
ui = [xi, vi]  # 2 変数の初期値
ti = 0  # 初期時刻
tf = 10  # 終了時刻
p = [m, k]  # パラメータ
prob = ODEProblem(HarmonicOscillator, ui, (ti,tf), p)  # 問題定義
Out[102]:
ODEProblem with uType Vector{Int64} and tType Int64. In-place: true
Non-trivial mass matrix: false
timespan: (0, 10)
u0: 2-element Vector{Int64}:
 1
 0
In [104]:
@time sol = solve(prob, Tsit5(), reltol=1e-8, abstol=1e-8);

  0.005909 seconds (13.70 k allocations: 650.750 KiB, 96.04% compilation time: 100% of which was recompilation)
In [46]:
plot(sol.t, sol[1,:], st=:scatter, xlabel="t", ylabel="x", label="numerical")  # t vs x でプロット
plot!(ti:0.01:tf, t -> cos(sqrt(k/m)t), label="analytic")  # 解析解 x = cos(sqrt(k/m)t) を重ねる
Out[46]:

問題¶

同じ単振動を初期条件 $x_\mathrm{i}=0$, $v_\mathrm{i}=1$ で解け. 解析解は何になるか.

In [50]:
xi = 0  # x の初期値
vi = 1  # v の初期値
prob = ODEProblem(HarmonicOscillator, [xi,vi], (ti,tf), p)  # 問題定義

@time sol = solve(prob, Tsit5(), reltol=1e-8, abstol=1e-8)

plot(sol.t, sol[1,:], st=:scatter, xlabel="t", ylabel="x", label="numerical")  # t vs x でプロット
plot!(ti:0.01:tf, t -> sin(sqrt(k/m)t), label="analytic")  # 解析解 x = sin(sqrt(k/m)t) を重ねる

  0.000104 seconds (2.06 k allocations: 90.891 KiB)
Out[50]:

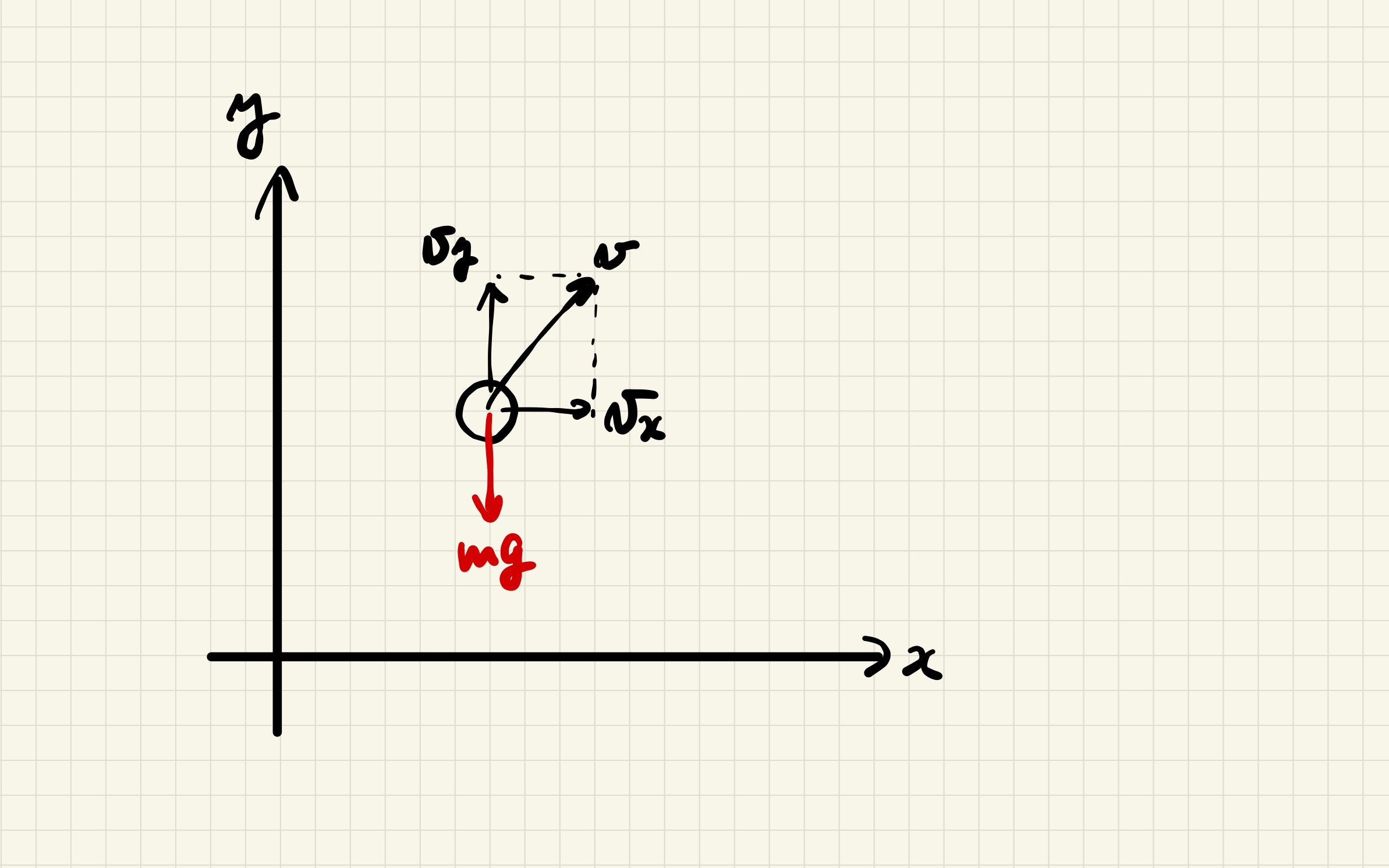
§2.2 放物¶

No description has been provided for this image

問題¶

投げ上げを初期位置 $(x_\mathrm{i},y_\mathrm{i})=(0,0)$, 初速 $(v_{x,\mathrm{i}},v_{y,\mathrm{i}})=(5,10)$ のもとで解き, $(x,y)$ 平面にプロットせよ. $m=1$, $g=9.8$ とする.

解答¶

運動方程式は $$\begin{cases} \dot{x}=v_x, \\ \dot{v}_x=0, \\ \dot{y}=v_y, \\ \dot{v}_y=-g, \end{cases}$$ である.

In [54]:
# 微分 du, 変数 u, パラメータ p, 時間 t
# u[1] = x, u[2] = vx, u[3] = y, u[4] = vy
# p = g
function Throw(du, u, p, t)
    du[1] = u[2]
    du[2] = 0
    du[3] = u[4]
    du[4] = -p
end

g = 9.8 # 重力加速度
    
xi = 0  # x の初期値
vxi = 5  # vx の初期値
yi = 0 # y の初期値
vyi = 10 # vy の初期値

ti = 0  # 初期時刻
tf = 2  # 終了時刻

prob = ODEProblem(Throw, [xi,vxi,yi,vyi], (ti,tf), g)  # 問題定義

@time sol = solve(prob, Tsit5(); reltol=1e-20, abstol=1e-20);

  0.935387 seconds (6.21 M allocations: 331.317 MiB, 9.79% gc time, 89.68% compilation time)
In [55]:
plot(sol[1,:], sol[3,:], xlabel="x", ylabel="y")
Out[55]:

§2.3 単振り子¶

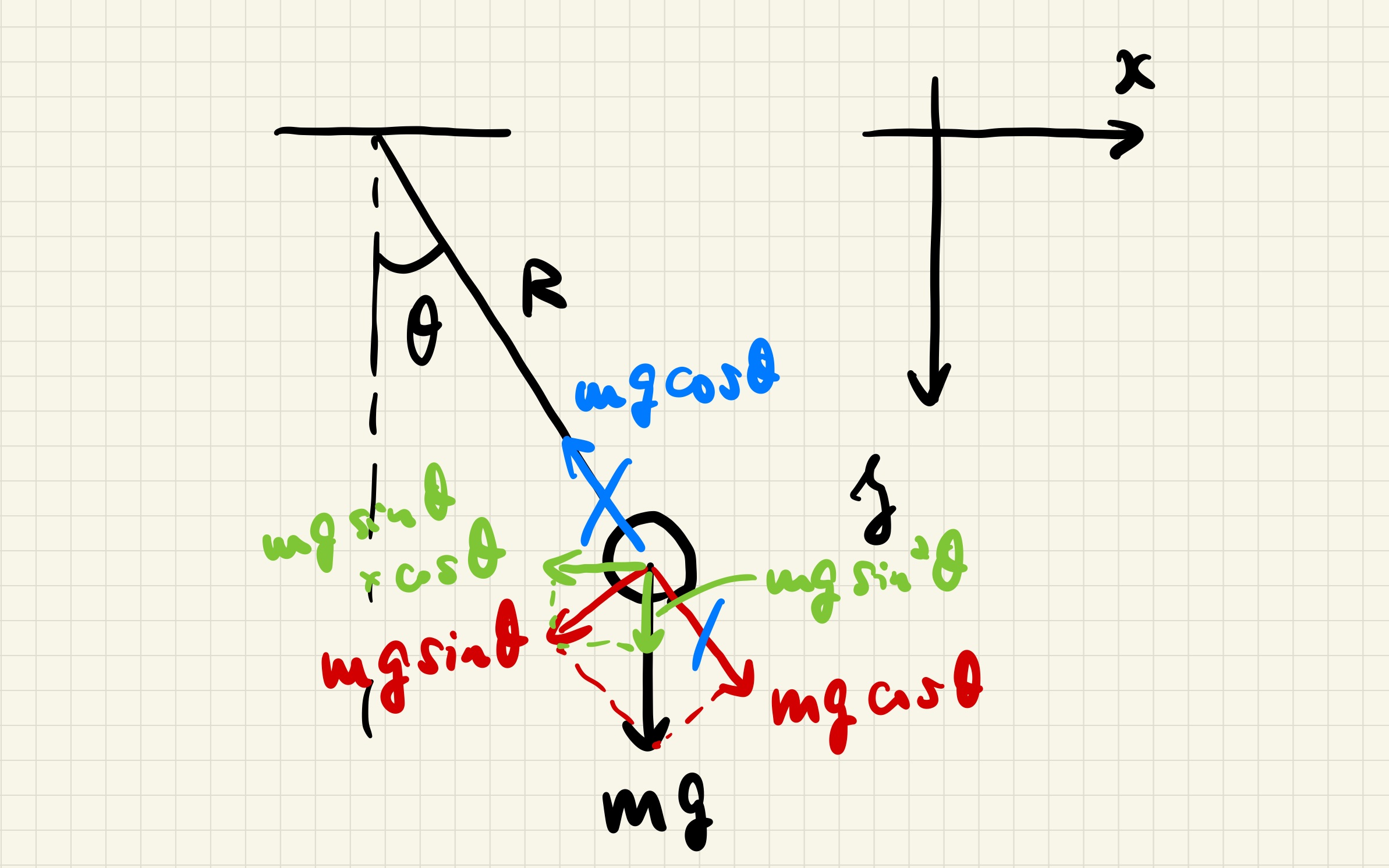No description has been provided for this image $$\begin{cases} \displaystyle m\ddot{x}=mR\partial_t^2\sin\theta=mR(\ddot{\theta}\cos\theta-\dot{\theta}^2\sin\theta)=-mg\sin\theta\cos\theta, \\ m\ddot{y}=mR\partial_t^2\cos\theta=mR(-\ddot{\theta}\sin\theta-\dot{\theta}^2\cos\theta)=mg\sin^2\theta. \end{cases}$$ まとめると $$R\ddot{\theta}=-g\sin\theta,$$ となる.
In [106]:
# 微分 du, 変数 u, パラメータ p, 時間 t
# u[1] = theta, u[2] = \dot{theta}
# p[1] = R, p[2] = g
function Pendulum(du, u, p, t)
    du[1] = u[2] # d theta / d t = vtheta
    du[2] = -p[2]/p[1]*sin(u[1]) # d vtheta / d t = - g/R * sin(theta)
end
Out[106]:
Pendulum (generic function with 1 method)
In [108]:
R = 1  # 腕の長さ
g = 9.8  # 重力加速度

θi = π/4  # theta の初期値
vθi = 0  # vtheta の初期値
ui = [θi, vθi]  # 2 変数の初期値
ti = 0  # 初期時刻
tf = 10  # 終了時刻
p = [R, g]  # パラメータ
prob = ODEProblem(Pendulum, ui, (ti,tf), p)  # 問題定義
Out[108]:
ODEProblem with uType Vector{Float64} and tType Int64. In-place: true
Non-trivial mass matrix: false
timespan: (0, 10)
u0: 2-element Vector{Float64}:
 0.7853981633974483
 0.0
In [66]:
@time sol = solve(prob, Tsit5(), reltol = 1e-8, abstol = 1e-8);

  0.000453 seconds (5.70 k allocations: 256.016 KiB)
In [68]:
plot(sol.t, sol[1,:], st=:scatter)
Out[68]:
In [72]:
# 描画設定
anim = @animate for t in ti:0.05:tf
    θ = sol(t)[1]
    x = R * sin(θ)
    y = R * cos(θ)

    plot([0, x], [0, -y],
         xlims = (-R-0.2, R+0.2),
         ylims = (-R-0.2, 0.2),
         lw=3, marker=:circle, markersize=8,
         legend=false, aspect_ratio=:equal,
         xlabel="x", ylabel="y", title=@sprintf("t = %.2f s", t))
end

# gifとして保存
gif(anim, "gifs/pendulum.gif", fps=20)

[ Info: Saved animation to /Users/yuichirotada/Documents/Univ/website/julia/gifs/pendulum.gif
Out[72]:
No description has been provided for this image

中間発表¶

好きな質点系をシミュレートしアニメーションを出力せよ

例 1: 2 重振り子¶

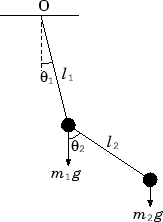No description has been provided for this image 二重振り子の運動方程式は $$\begin{cases} \dot{\theta}_1=v_1, \\ \dot{\theta}_2=v_2, \\ \displaystyle \dot{v}_1=\frac{g(C\sin\theta_2-\frac{m_{12}}{m_2}\sin\theta_1)-(l_1v_1^2C+l_2v_2^2)S}{l_1(\frac{m_{12}}{m_2}-C^2)}, \\ \displaystyle \dot{v}_2=\frac{g\frac{m_{12}}{m_2}(C\sin\theta_1-\sin\theta_2)+(\frac{m_{12}}{m_2}l_1v_1^2+l_2v_2^2C)S}{l_2(\frac{m_{12}}{m_2}-C^2)}, \end{cases}$$ で与えられる (https://www.aihara.co.jp/~taiji/pendula-equations/present-node2.html 参照). ここで $C=\cos(\theta_1-\theta_2)$, $S=\sin(\theta_1-\theta_2)$, $m_{12}=m_1+m_2$ である.

例 2: ローレンツアトラクター¶

$$\begin{cases} \displaystyle \frac{\mathrm{d}x}{\mathrm{d}t}=\sigma(y-x), \\[5pt] \displaystyle \frac{\mathrm{d}y}{\mathrm{d}t}=x(\rho-z)-y, \\[5pt] \displaystyle \frac{\mathrm{d}z}{\mathrm{d}t}=xy-\beta z. \end{cases}$$ $\sigma$, $\rho$, $\beta$ は正のパラメータ.

例 3: $N$ ($\geq3$) 体万有引力シミュレーション¶

$$\begin{cases} \displaystyle \ddot{x}_i=\sum_{j\neq i}m_j\frac{x_j-x_i}{r_{ij}^3}, \\ \displaystyle \ddot{y}_i=\sum_{j\neq i}m_j\frac{y_j-y_i}{r_{ij}^3}, \\ \displaystyle \ddot{z}_i=\sum_{j\neq i}m_j\frac{z_j-z_i}{r_{ij}^3}, \end{cases}$$ ただし $$r_{ij}=\sqrt{(x_i-x_j)^2+(y_i-y_j)^2+(z_i-z_j)^2}.$$

例 1: 解答例¶

In [110]:
# 微分 du, 変数 u, パラメータ p, 時間 t
# u[1] = theta1, u[2] = v1, u[3] = theta2, u[4] = v2
# p[1] = l1, p[2] = l2, p[3] = m1, p[4] = m2, p[5] = g
function DoublePendulum(du, u, p, t)
    theta1 = u[1]
    v1 = u[2]
    theta2 = u[3]
    v2 = u[4]
    l1 = p[1]
    l2 = p[2]
    m1 = p[3]
    m2 = p[4]
    g = p[5]

    C = cos(theta1-theta2)
    S = sin(theta1-theta2)
    m12 = m1+m2
    
    du[1] = v1
    du[2] = (g*(C*sin(theta2)-m12/m2*sin(theta1)) - (l1*v1*v1*C + l2*v2*v2)*S) / l1 / (m12/m2 - C*C)
    du[3] = v2
    du[4] = (g*m12/m2*(C*sin(theta1)-sin(theta2)) + (m12/m2*l1*v1*v1 + l2*v2*v2*C)*S) / l2 / (m12/m2 - C*C)
end
Out[110]:
DoublePendulum (generic function with 1 method)
In [112]:
l1 = 1 
l2 = 1
m1 = 1
m2 = 1
g = 9.8
    
theta1i = π/2
v1i = 0
theta2i = π/2
v2i = 0
ti = 0
tf = 25
p = [l1,l2,m1,m2,g]

ui0 = [theta1i, v1i, theta2i, v2i]
ui1 = [theta1i, v1i, theta2i + 1e-5, v2i]
ui2 = [theta1i, v1i, theta2i - 1e-5, v2i]
prob0 = ODEProblem(DoublePendulum, ui0, (ti,tf), p)
prob1 = ODEProblem(DoublePendulum, ui1, (ti,tf), p)
prob2 = ODEProblem(DoublePendulum, ui2, (ti,tf), p)
Out[112]:
ODEProblem with uType Vector{Float64} and tType Int64. In-place: true
Non-trivial mass matrix: false
timespan: (0, 25)
u0: 4-element Vector{Float64}:
 1.5707963267948966
 0.0
 1.5707863267948965
 0.0
In [118]:
@time begin
    sol0 = solve(prob0, Tsit5(); reltol = 1e-8, abstol = 1e-8)
    sol1 = solve(prob1, Tsit5(); reltol = 1e-8, abstol = 1e-8)
    sol2 = solve(prob2, Tsit5(); reltol = 1e-8, abstol = 1e-8)
end;

  0.046810 seconds (269.39 k allocations: 14.073 MiB, 89.89% compilation time)
In [122]:
# 描画設定
anim = @animate for t in ti:0.05:tf
    θ1 = sol0(t)[1]
    θ2 = sol0(t)[3]
    x1 = l1 * sin(θ1)
    y1 = l1 * cos(θ1)
    x2 = x1 + l2 * sin(θ2)
    y2 = y1 + l2 * cos(θ2)

    plot([0, x1, x2], [0, -y1, -y2],
         xlims = (-l1-l2-0.2, l1+l2+0.2),
         ylims = (-l1-l2-0.2, l1+l2+0.2),
         lw=3, marker=:circle, markersize=8,
         legend=false, aspect_ratio=:equal,
         xlabel="x", ylabel="y", title=@sprintf("t = %.2f s", t))

    θ1 = sol1(t)[1]
    θ2 = sol1(t)[3]
    x1 = l1 * sin(θ1)
    y1 = l1 * cos(θ1)
    x2 = x1 + l2 * sin(θ2)
    y2 = y1 + l2 * cos(θ2)

    plot!([0, x1, x2], [0, -y1, -y2],
         xlims = (-l1-l2-0.2, l1+l2+0.2),
         ylims = (-l1-l2-0.2, l1+l2+0.2),
         lw=3, marker=:circle, markersize=8,
         legend=false)

    θ1 = sol2(t)[1]
    θ2 = sol2(t)[3]
    x1 = l1 * sin(θ1)
    y1 = l1 * cos(θ1)
    x2 = x1 + l2 * sin(θ2)
    y2 = y1 + l2 * cos(θ2)

    plot!([0, x1, x2], [0, -y1, -y2],
         xlims = (-l1-l2-0.2, l1+l2+0.2),
         ylims = (-l1-l2-0.2, l1+l2+0.2),
         lw=3, marker=:circle, markersize=8,
         legend=false)
end

# gifとして保存
gif(anim, "gifs/double_pendulum.gif", fps=20)

[ Info: Saved animation to /Users/yuichirotada/Documents/Univ/website/julia/gifs/double_pendulum.gif
Out[122]:
No description has been provided for this image

例 2: 解答例¶

In [124]:
function Lorenz(du, u, p, t)
    du[1] = p[1]*(u[2]-u[1])
    du[2] = u[1]*(p[2]-u[3]) - u[2]
    du[3] = u[1]*u[2] - p[3]*u[3]
end
Out[124]:
Lorenz (generic function with 2 methods)
In [126]:
σ = 10
ρ = 28
β = 8/3

ti = 0
tf = 50

ui0 = [-10,-10,30]
uip = [-10+1e-5,-10+1e-5,30+1e-5]
uim = [-10-1e-5,-10-1e-5,30-1e-5]

prob0 = ODEProblem(Lorenz, ui0, (ti,tf), [σ,ρ,β])
probp = ODEProblem(Lorenz, uip, (ti,tf), [σ,ρ,β])
probm = ODEProblem(Lorenz, uim, (ti,tf), [σ,ρ,β])
Out[126]:
ODEProblem with uType Vector{Float64} and tType Int64. In-place: true
Non-trivial mass matrix: false
timespan: (0, 50)
u0: 3-element Vector{Float64}:
 -10.00001
 -10.00001
  29.99999
In [130]:
@time begin 
    sol0 = solve(prob0, Tsit5(); dt = 0.01, adaptive=false) # 固定幅で解く
    solp = solve(probp, Tsit5(); dt = 0.01, adaptive=false)
    solm = solve(probm, Tsit5(); dt = 0.01, adaptive=false)
end;

  0.143964 seconds (656.87 k allocations: 32.537 MiB, 95.97% compilation time)
In [132]:
anim = @animate for i in 1:10:length(sol0.u)
    plot(sol0[1,max(1,i-500):i], sol0[2,max(1,i-500):i], sol0[3,max(1,i-500):i],
        xlims = (-20,20), ylims = (-30,30), zlims = (-20,50),
        title=@sprintf("t = %.2f s", sol0.t[i]))
    plot!(solp[1,max(1,i-500):i], solp[2,max(1,i-500):i], solp[3,max(1,i-500):i])
    plot!(solm[1,max(1,i-500):i], solm[2,max(1,i-500):i], solm[3,max(1,i-500):i])
end

gif(anim, "gifs/Lorenz.gif", fps=20)

[ Info: Saved animation to /Users/yuichirotada/Documents/Univ/website/julia/gifs/Lorenz.gif
Out[132]:
No description has been provided for this image

例 3: 解答例¶

In [134]:
# xy 平面のみ
# u[4i-3] = xi, u[4i-2] = yi, u[4i-1] = vxi, u[4i] = vyi
# p[i] = mi
function Nbody(du,u,p,t)
    for i in 1:div(length(u),4)
        du[4i-3] = u[4i-1]
        du[4i-2] = u[4i]

        du[4i-1] = 0
        du[4i] = 0
        
        for j in 1:div(length(u),4)
            if i == j
                continue
            end
            
            rijvec = u[4j-3:4j-2]-u[4i-3:4i-2]
            rij = norm(rijvec)

            du[4i-1] += p[j]*rijvec[1]/rij^3
            du[4i] += p[j]*rijvec[2]/rij^3
        end
    end
end
Out[134]:
Nbody (generic function with 1 method)
In [144]:
Np = 3

u0 = [4,0,0,0, 1,1,0,0, -1,-1,0,0]
up = [4,0,0,0, 1+1e-3,1,0,0, -1,-1,0,0]
um = [4,0,0,0, 1-1e-3,1,0,0, -1,-1,0,0]
tf = 50
mass = [1 for i in 1:Np]

prob0 = ODEProblem(Nbody,u0,(0,tf),mass)
probp = ODEProblem(Nbody,up,(0,tf),mass)
probm = ODEProblem(Nbody,um,(0,tf),mass);
In [146]:
@time begin 
    sol0 = solve(prob0, Tsit5(), reltol=1e-8, abstol=1e-8)
    solp = solve(probp, Tsit5(), reltol=1e-8, abstol=1e-8)
    solm = solve(probm, Tsit5(), reltol=1e-8, abstol=1e-8)
end;

  0.709019 seconds (14.11 M allocations: 580.464 MiB, 58.98% gc time)
In [148]:
# 描画設定
lim = 5
anim = @animate for t in ti:0.1:tf
    plot([sol0(t)[i] for i in 1:4:4Np], [sol0(t)[i] for i in 2:4:4Np],
         xlims = (-lim, lim),
         ylims = (-lim, lim),
         marker=:circle, markersize=5, st=:scatter,
         legend=false, aspect_ratio=:equal,
         xlabel="x", ylabel="y", title=@sprintf("t = %.2f s", t))
    plot!([solp(t)[i] for i in 1:4:4Np], [solp(t)[i] for i in 2:4:4Np],
        marker=:circle, markersize=5, st=:scatter)
    plot!([solm(t)[i] for i in 1:4:4Np], [solm(t)[i] for i in 2:4:4Np],
        marker=:circle, markersize=5, st=:scatter)
end

# gifとして保存
gif(anim, "gifs/Nbody.gif", fps=20)

[ Info: Saved animation to /Users/yuichirotada/Documents/Univ/website/julia/gifs/Nbody.gif
Out[148]:
No description has been provided for this image

§3 解析力学¶

§3.1 最速降下曲線¶

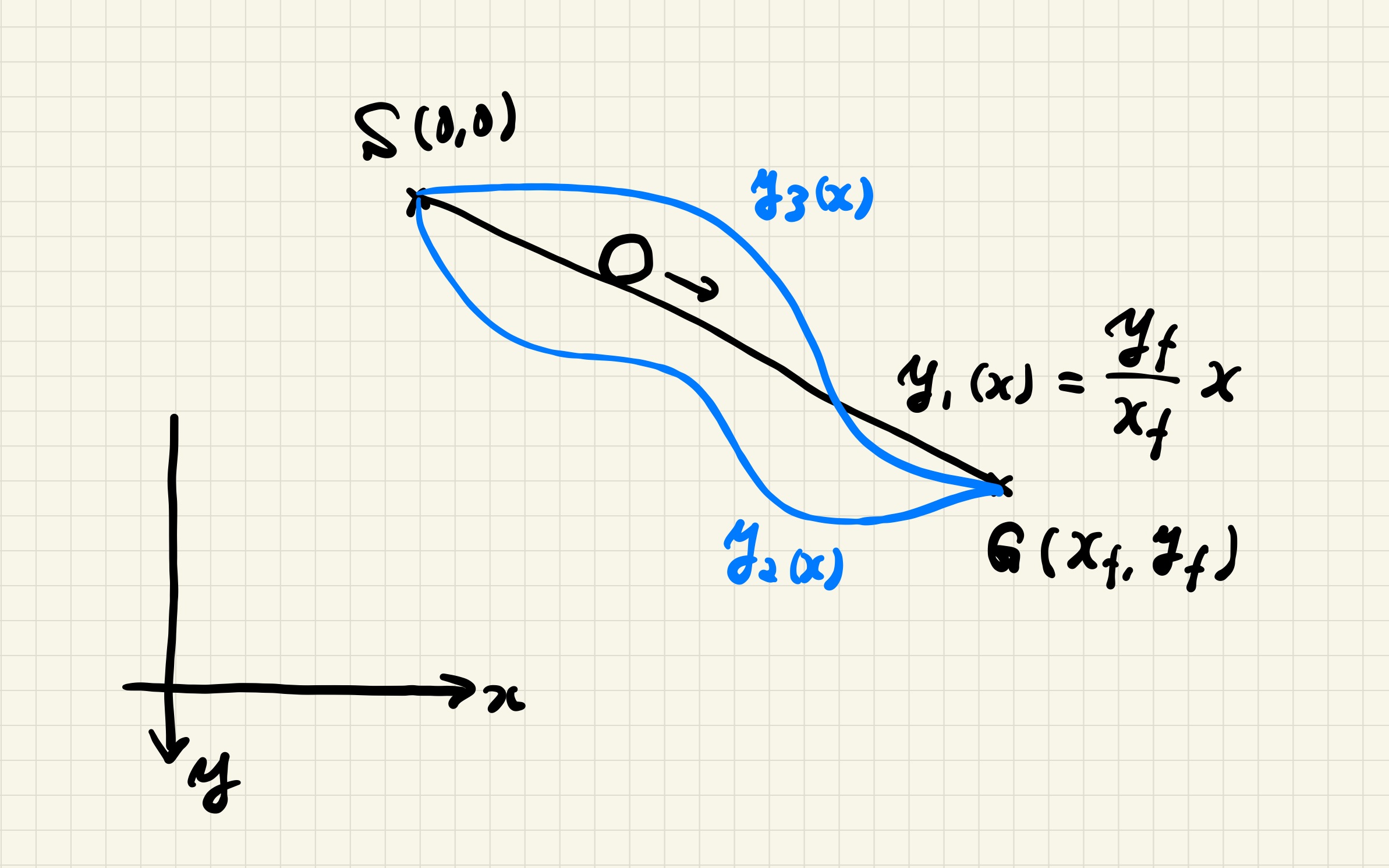No description has been provided for this image 原点 $S(0,0)$ からゴール $G(x_\mathrm{f},y_\mathrm{f})$ まで、とある曲線 $y(x)$ に沿って物を転がすことを考える. 初速は $0$ とする. どういう曲線 $y(x)$ なら「最速」で $G$ までたどり着くであろうか.
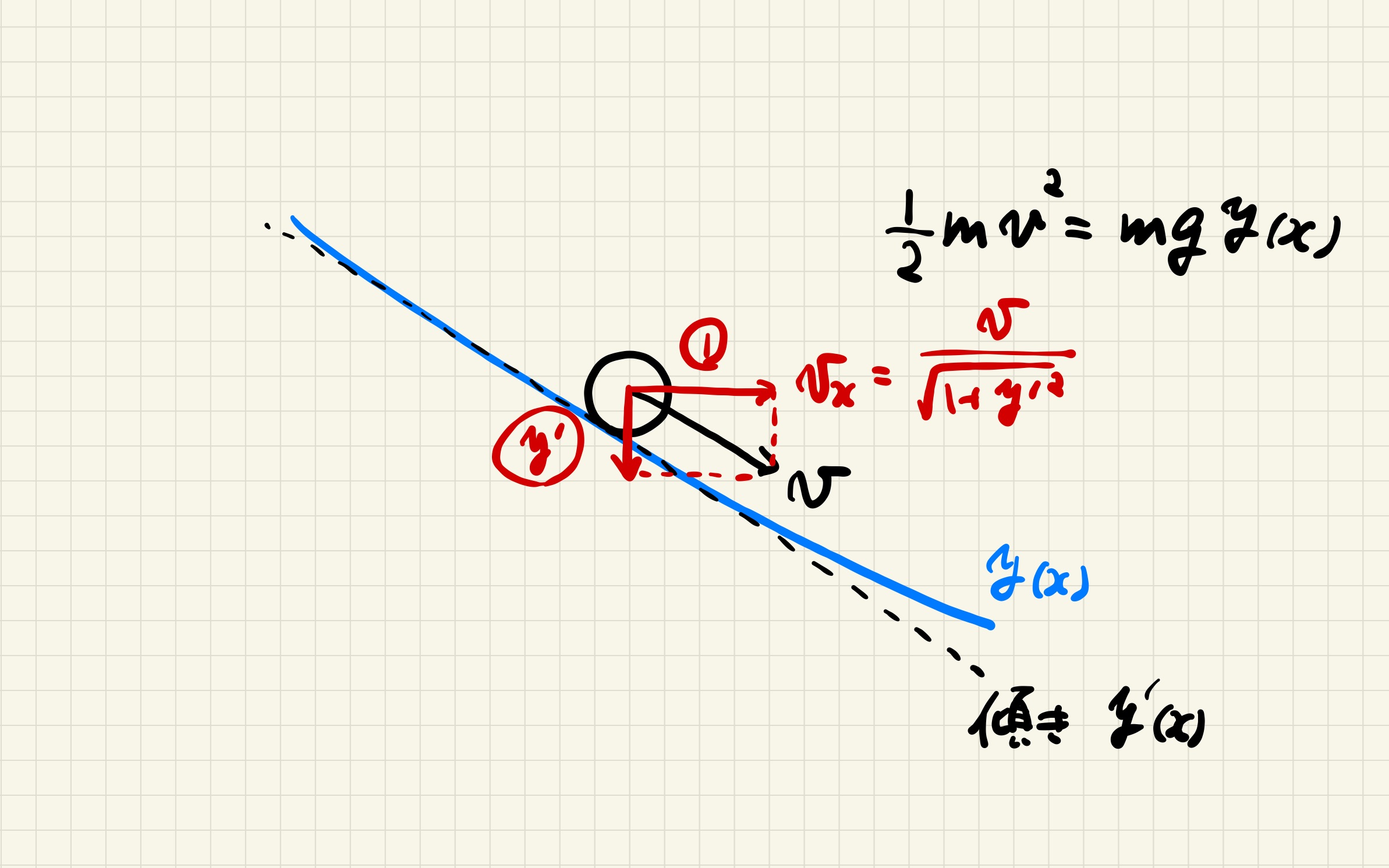No description has been provided for this image ある点 $y(x)$ において速度 $v$ はエネルギー保存より $$\frac{1}{2}mv^2=mgy(x) \,\Leftrightarrow\, v=\sqrt{2gy(x)}.$$ 曲線 $y(x)$ に沿わないといけないので, $x$ 方向の速度は $$v_x=\dot{x}=\frac{1}{\sqrt{1+y'(x)^2}}v=\sqrt{\frac{2gy(x)}{1+y'(x)^2}}, \tag{4}$$ となる.

§3.1.1 3 つの例¶

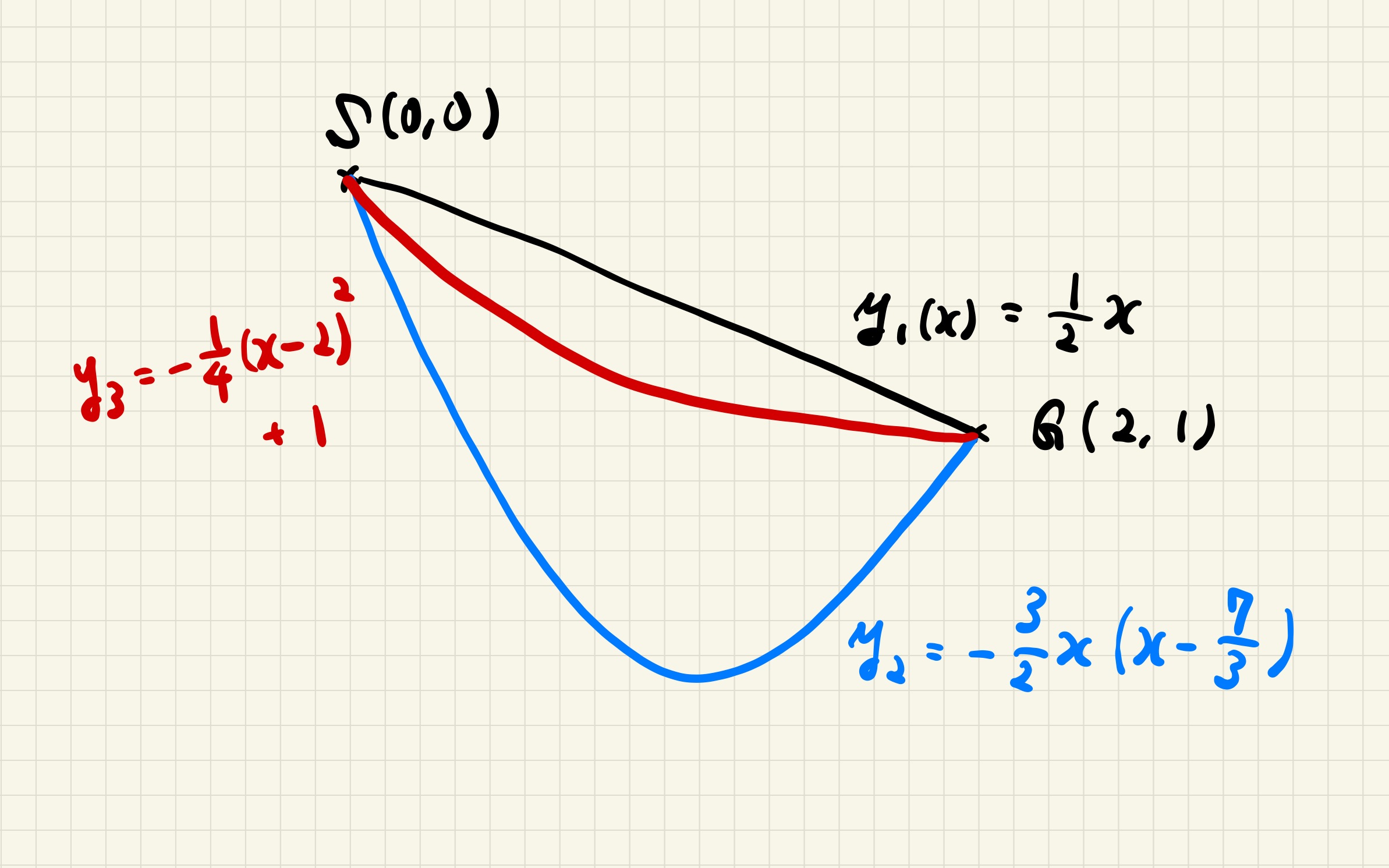
No description has been provided for this image
In [150]:
y1(x) = x/2
y2(x) = -3/2*x*(x-7/3)
y3(x) = -(x-2)^2/4 + 1.

g = 9.8
Out[150]:
9.8
In [164]:
yoff = 0.1 # 原点で初速がないとプログラム上動かないので少しかさまし

vx1(x) = sqrt(2g*(y1(x)+yoff) / (1+ForwardDiff.derivative(y1,x)^2))
vx2(x) = sqrt(2g*(y2(x)+yoff) / (1+ForwardDiff.derivative(y2,x)^2))
vx3(x) = sqrt(2g*(y3(x)+yoff) / (1+ForwardDiff.derivative(y3,x)^2))

xi = 0
xf = 2

function brachistochrone(du,u,p,t)
    if u[1] < xf
        du[1] = vx1(u[1])
    else
        du[1] = 0 # xf を越えたら止める
    end

    if u[2] < xf
        du[2] = vx2(u[2])
    else
        du[2] = 0 # xf を越えたら止める
    end

    if u[3] < xf
        du[3] = vx3(u[3])
    else
        du[3] = 0 # xf を越えたら止める
    end
end

ti = 0
tf = 1.5
prob = ODEProblem(brachistochrone, [xi,xi,xi], (ti,tf))
Out[164]:
ODEProblem with uType Vector{Int64} and tType Float64. In-place: true
Non-trivial mass matrix: false
timespan: (0.0, 1.5)
u0: 3-element Vector{Int64}:
 0
 0
 0
In [166]:
@time sol = solve(prob, Tsit5(); reltol=1e-8, abstol=1e-8); 

  0.031474 seconds (37.88 k allocations: 1.198 MiB, 96.87% compilation time: 100% of which was recompilation)
In [168]:
xlist = [x for x in 0:0.01:2]; # プロット用 x リスト

# 描画設定
anim = @animate for t in ti:0.01:tf
    x1t, x2t, x3t = sol(t)
    y1t = -y1(x1t)
    y2t = -y2(x2t)
    y3t = -y3(x3t)

    plot([x1t], [y1t],
         xlims = (-0.2, 2+0.2),
         ylims = (-2-0.2, 0.2),
         marker=:circle, markersize=8, primary=false,
         xlabel="x", ylabel="y", title=@sprintf("t = %.2f s", t), aspect_ratio=:equal)
    plot!([x2t],[y2t],marker=:circle, markersize=8, primary=false)
    plot!([x3t],[y3t],marker=:circle, markersize=8, primary=false)
    plot!(xlist, -y1.(xlist), label="y1")
    plot!(xlist, -y2.(xlist), label="y2")
    plot!(xlist, -y3.(xlist), label="y3")
end

# gifとして保存
gif(anim, "gifs/brachistochrone.gif", fps=30)

[ Info: Saved animation to /Users/yuichirotada/Documents/Univ/website/julia/gifs/brachistochrone.gif
Out[168]:
No description has been provided for this image

問題¶

最速で到達する関数形 $y_\mathrm{fast}(x)$ を探してみよう.

§3.1.2 最小時間問題¶

$x$ における $x$ 方向の速度 $v_x$ は (4) 式で与えられるので, 微小区間 $(x,x+\mathrm{d}x)$ の間にかかる微小時間 $\mathrm{d}t$ は $$\mathrm{d}t=\frac{\mathrm{d}x}{v_x}=\sqrt{\frac{1+y'(x)^2}{2gy(x)}}\mathrm{d}x,$$ で与えられる. これを積分の変数変換の式だと考えれば, 到達時間 $T$ は以下の積分で与えられることになる. $$T[y(x)] = \int_0^T\mathrm{d}t = \int_0^{x_\mathrm{f}}\frac{1}{v_x}\mathrm{d}x = \int_0^{x_\mathrm{f}}\sqrt{\frac{1+y'(x)^2}{2gy(x)}}\mathrm{d}x.$$ 到達時間 $T$ は曲線の方程式 $y(x)$ を 1 つ与えると値が 1 つ決まる. このように関数形を与えると 1 つ値を返す変換を「汎函数」と呼び, $T[y(x)]$ のように $[]$ を使って表す.

In [170]:
function arrivalT(vx::Function, xi, xf)
    return quadgk(x -> 1/vx(x), xi, xf)[1] # 1/vx を xi から xf まで積分する
end
Out[170]:
arrivalT (generic function with 1 method)
In [172]:
@show arrivalT(vx1, xi, xf)
@show arrivalT(vx2, xi, xf)
@show arrivalT(vx3, xi, xf)

arrivalT(vx1, xi, xf) = 0.7400186442279827
arrivalT(vx2, xi, xf) = 0.8392208962277332
arrivalT(vx3, xi, xf) = 0.6774096266267688
Out[172]:
0.6774096266267688

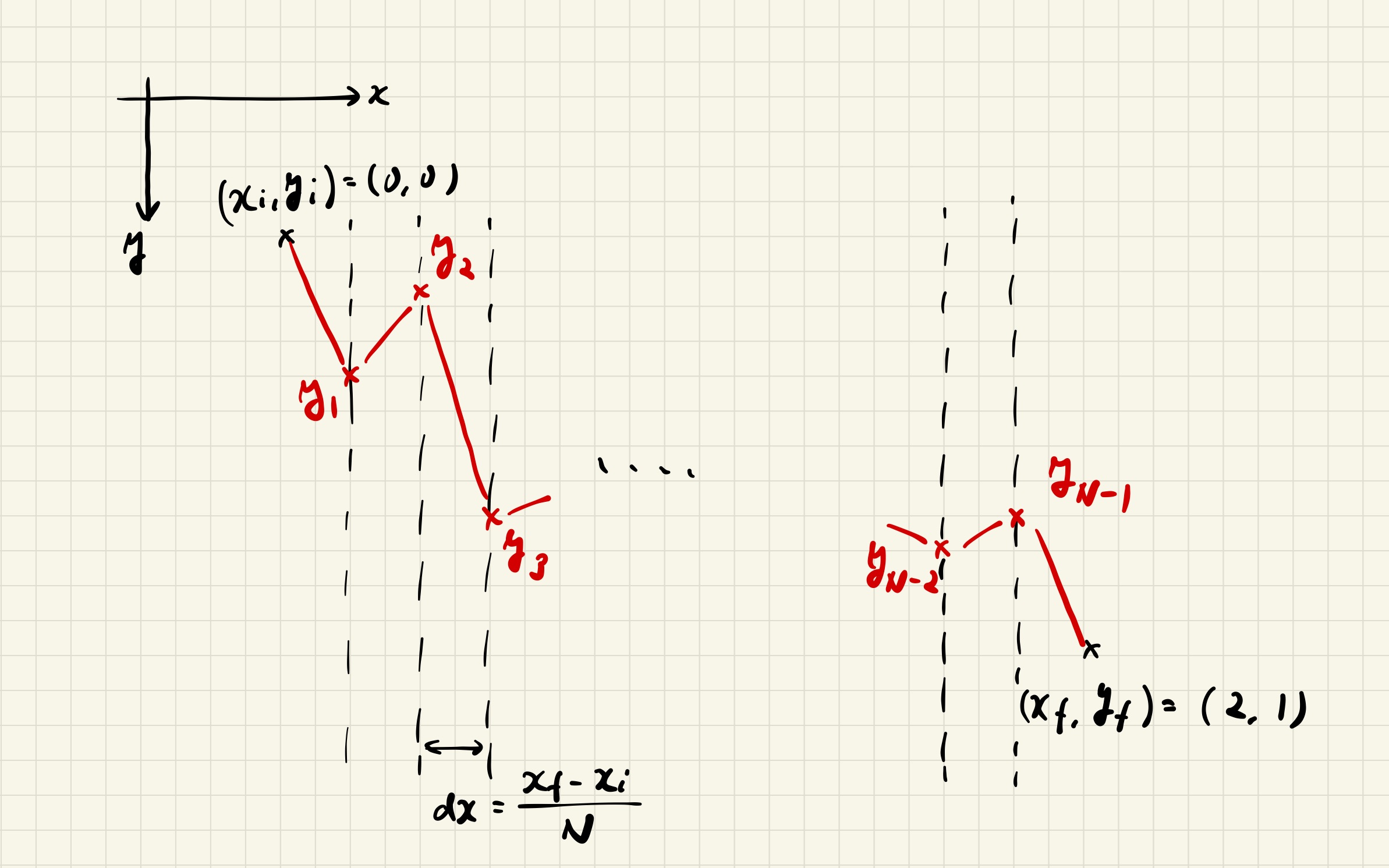$T[y(x)]$ が最小となる $y(x)$ はどうすればもとまるだろうか. 数値的には次のようにすればよい. No description has been provided for this image $x_\mathrm{i}$ における $y$ は $y_\mathrm{i}$, 曲線の傾きは $y'_\mathrm{i}\coloneqq(y_1-y_\mathrm{i})/\mathrm{d}x$. したがって次の $x_1$ までかかる時間 $\mathrm{d}T_\mathrm{i}$ は $$\mathrm{d}T_\mathrm{i}=\sqrt{\frac{1+{y'_\mathrm{i}}^2}{2gy_\mathrm{i}}}\mathrm{d}x.$$ 同様に $x_n$ ($n=1,2,\dots,N-2$) において次の点までかかる時間は $$\mathrm{d}T_n=\sqrt{\frac{1+{y'_n}^2}{2gy_n}}\mathrm{d}x, \quad y'_n=\frac{y_{n+1}-y_n}{\mathrm{d}x}.$$ $x_{N-1}$ では $$\mathrm{d}T_{N-1}=\sqrt{\frac{1+{y'_{N-1}}^2}{2gy_{N-1}}}\mathrm{d}x, \quad y'_{N-1}=\frac{y_\mathrm{f}-y_{N-1}}{\mathrm{d}x}.$$ $x_N=x_\mathrm{f}$ はすでにゴールに到着しているので考慮しない. 以上より適当に与えたリスト $\mathbf{y}=[y_1,y_2,\dots,y_{N-1}]$ に対し到達時間は $$T[\mathbf{y}]=\mathrm{d}T_\mathrm{i}+\sum_{n=1}^{N-2}\mathrm{d}T_n+\mathrm{d}T_{N-1},$$ と計算できる. これを最小化するよう $y_n$ を 1 つずつ合わせる (南京錠を開けるように) ことを繰り返していけば, 真の解 $y(x)$ に近づく.

In [174]:
xi = 0
xf = 2
N = 100+1 # x 分割数
dx = (xf-xi) / N
yi = 0
yf = 1

function arrivalT(y::Vector) # y は長さ N-1 のリスト
    yprime = diff(y) ./ dx # y[n+1] - y[n] のリスト
    ypi = (y[1] - yi) /dx
    ypf = (yf - y[end]) / dx
    T = (sqrt((1+ypi^2)/2/g/(yi+yoff)) # dTi
        + sum([sqrt((1+yprime[i]^2)/2/g/(y[i]+yoff)) for i in 1:length(y)-1]) # dTn
        + sqrt((1+ypf^2)/2/g/(y[end]+yoff)))*dx # dT(N-1)
    return T
end
Out[174]:
arrivalT (generic function with 2 methods)
In [176]:
y0 = [y1(x) for x in dx:dx:xf-dx] # 初期試行リストとしては直線 y(x) = y1(x) = x/2 を用いよう
arrivalT(y0) # y1(x) に対する近似到着時間
Out[176]:
0.7456049262661909
In [178]:
opt_result = optimize(arrivalT, y0, BFGS())  # BFGS法で最適化する準備
y_opt = opt_result.minimizer # T を最小にする y を求める

xlist = [x for x in 0:0.01:2]

# 結果プロット
plot(xi:dx:xf, vcat([-yi],-y_opt,[-yf]), label="opt", aspect_ratio=:equal, xlabel="x", ylabel="y")
plot!(xlist, -y1.(xlist), label="y1", line=:auto)
plot!(xlist, -y2.(xlist), label="y2", line=:auto)
plot!(xlist, -y3.(xlist), label="y3", line=:auto)
Out[178]:
In [182]:
y_opt_int = CubicSplineInterpolation(xi:dx:xf, vcat([yi],y_opt,[yf])) # 滑らかにつなぐ

plot(xi:dx:xf, (x -> -y_opt_int(x)), label="opt", aspect_ratio=:equal, xlabel="x", ylabel="y") # 同じ図が得られる
plot!(xlist, -y1.(xlist), label="y1", line=:auto)
plot!(xlist, -y2.(xlist), label="y2", line=:auto)
plot!(xlist, -y3.(xlist), label="y3", line=:auto)
Out[182]:
In [186]:
yoff = 0.1 # 原点で初速がないとプログラム上動かないので少しかさまし

vx1(x) = sqrt(2g*(y1(x)+yoff) / (1+ForwardDiff.derivative(y1,x)^2))
vx2(x) = sqrt(2g*(y2(x)+yoff) / (1+ForwardDiff.derivative(y2,x)^2))
vx3(x) = sqrt(2g*(y3(x)+yoff) / (1+ForwardDiff.derivative(y3,x)^2))
vx_opt(x) = sqrt(2g*(y_opt_int(x)+yoff) / (1+ForwardDiff.derivative(y_opt_int,x)^2))

xi = 0
xf = 2

function brachistochrone(du,u,p,t)
    if u[1] < xf
        du[1] = vx1(u[1])
    else
        du[1] = 0 # xf を越えたら止める
    end

    if u[2] < xf
        du[2] = vx2(u[2])
    else
        du[2] = 0 # xf を越えたら止める
    end

    if u[3] < xf
        du[3] = vx3(u[3])
    else
        du[3] = 0 # xf を越えたら止める
    end

    if u[4] < xf
        du[4] = vx_opt(u[4])
    else
        du[4] = 0 # xf を越えたら止める
    end
end

ti = 0
tf = 1.5
prob = ODEProblem(brachistochrone, [xi,xi,xi,xi], (ti,tf))
Out[186]:
ODEProblem with uType Vector{Int64} and tType Float64. In-place: true
Non-trivial mass matrix: false
timespan: (0.0, 1.5)
u0: 4-element Vector{Int64}:
 0
 0
 0
 0
In [188]:
@time sol = solve(prob, Tsit5(); reltol=1e-8, abstol=1e-8); 

  0.131399 seconds (822.82 k allocations: 39.412 MiB, 99.18% compilation time: 25% of which was recompilation)
In [190]:
xlist = [x for x in 0:0.01:2]; # プロット用 x リスト

# 描画設定
anim = @animate for t in ti:0.01:tf
    x1t, x2t, x3t, x4t = sol(t)
    y1t = -y1(x1t)
    y2t = -y2(x2t)
    y3t = -y3(x3t)
    x_opt_t = min(x4t,2)
    y_opt_t = -y_opt_int(x_opt_t)

    plot([x1t], [y1t],
        xlims = (-0.2, 2+0.2),
        ylims = (-2-0.2, 0.2),
        marker=:circle, markersize=8,
        xlabel="x", ylabel="y", title=@sprintf("t = %.2f s", t), 
        aspect_ratio=:equal, primary=false)
    plot!([x2t],[y2t],marker=:circle, markersize=8, primary=false)
    plot!([x3t],[y3t],marker=:circle, markersize=8, primary=false)
    plot!([x_opt_t],[y_opt_t],marker=:circle, markersize=8, primary=false)
    plot!(xlist, -y_opt_int.(xlist), label="y_opt")
    plot!(xlist, -y1.(xlist), line=:auto, label="y1")
    plot!(xlist, -y2.(xlist), line=:auto, label="y2")
    plot!(xlist, -y3.(xlist), line=:auto, label="y3")
end

# gifとして保存
gif(anim, "gifs/brachistochrone_opt.gif", fps=30)

[ Info: Saved animation to /Users/yuichirotada/Documents/Univ/website/julia/gifs/brachistochrone_opt.gif
Out[190]:
No description has been provided for this image
In [192]:
@show arrivalT(vx1, xi, xf)
@show arrivalT(vx2, xi, xf)
@show arrivalT(vx3, xi, xf)
@show arrivalT(vx_opt, xi, xf)

arrivalT(vx1, xi, xf) = 0.7400186442279827
arrivalT(vx2, xi, xf) = 0.8392208962277332
arrivalT(vx3, xi, xf) = 0.6774096266267688
arrivalT(vx_opt, xi, xf) = 0.6627676593799467
Out[192]:
0.6627676593799467

§3.1.3 最小汎函数問題¶

結局 $T[y(x)]$ のような汎函数を最小化する $y_\mathrm{min}(x)$ はどのような関数だったのか. 例えば関数 $f(x)$ を最小化する点 $x_\mathrm{min}$ は $\mathrm{d}f/\mathrm{d}x=0$ となる点を求めればよい. これは $x_\mathrm{min}$ 付近では $x$ をわずかに ($\mathrm{d}x$) 動かしても $f$ が変わらないことを意味する. $$f(x_\mathrm{min}+\mathrm{d}x)\approx f(x_\mathrm{min}).$$ 汎函数においても $y_\mathrm{min}(x)$ を少しずらした経路 $y_\mathrm{min}(x)+\delta y(x)$ に対しても $T$ があまり変わらないはずだ: $$T[y_\mathrm{min}(x)+\delta y(x)]\approx T[y_\mathrm{min}].$$ この条件を満たす $y_\mathrm{min}(x)$ を見つけてくればよい.

到達時間 $T[y(x)]=\int_0^{x_\mathrm{f}}\sqrt{\frac{1+y'(x)^2}{2gy(x)}}\mathrm{d}x$ で具体的に考えてみよう. ずらした経路の微分が $y_\mathrm{min}'(x)+\delta y'(x)$ で与えられることに注意して \begin{align} T[y_\mathrm{min}(x)+\delta y(x)]&=\int_0^{x_\mathrm{f}}\mathrm{d}x\sqrt{\frac{1+(y_\mathrm{min}'(x)+\delta y'(x))^2}{2g(y_\mathrm{min}(x)+\delta y(x))}} \\ &\simeq\int_0^{x_\mathrm{f}}\mathrm{d}x\sqrt{\frac{1+(y_\mathrm{min}'(x))^2+2y_\mathrm{min}'(x)\delta y'(x)}{2g(y_\mathrm{min}(x)+\delta y(x))}} \quad \left(\text{$\because$ $(\delta y'(x))^2$ を無視}\right) \\ &=\int_0^{x_\mathrm{f}}\mathrm{d}x\sqrt{1+(y_\mathrm{min}'(x))^2}\times\left(1+\frac{2y_\mathrm{min}'(x)\delta y'(x)}{1+(y_\mathrm{min}'(x))^2}\right)^{1/2}\times\frac{1}{\sqrt{2gy_\mathrm{min}(x)}}\times\left(1+\frac{\delta y(x)}{y_\mathrm{min}(x)}\right)^{-1/2} \\ &\simeq\int_0^{x_\mathrm{f}}\mathrm{d}x\sqrt{\frac{1+(y_\mathrm{min}'(x))^2}{2gy_\mathrm{min}(x)}}\times\left(1+\frac{1}{2}\frac{2y_\mathrm{min}'(x)\delta y'(x)}{1+(y_\mathrm{min}'(x))^2}\right)\times\left(1-\frac{1}{2}\frac{\delta y(x)}{y_\mathrm{min}(x)}\right) \quad \left(\text{$\because$ $(1+\epsilon)^{1/2}\simeq1+\frac{1}{2}\epsilon$, $(1+\epsilon)^{-1/2}=(1-\frac{1}{2}\epsilon)$}\right) \\ &\simeq\int_0^{x_\mathrm{f}}\mathrm{d}x\sqrt{\frac{1+(y_\mathrm{min}'(x))^2}{2gy_\mathrm{min}(x)}}\times\left(1+\frac{y_\mathrm{min}'(x)\delta y'(x)}{1+(y_\mathrm{min}'(x))^2}-\frac{\delta y(x)}{2y_\mathrm{min}(x)}\right) \quad \left(\text{$\because$ $\delta y(x)\delta y'(x)$ を無視}\right) \\ &=T[y_\mathrm{min}(x)]+\int_0^{x_\mathrm{f}}\mathrm{d}x\left(\sqrt{\frac{1+(y_\mathrm{min}'(x))^2}{2gy_\mathrm{min}(x)}}\frac{y_\mathrm{min}'(x)}{1+(y_\mathrm{min}'(x))^2}\right)\delta y'(x)-\int_0^{x_\mathrm{f}}\mathrm{d}x\left(\sqrt{\frac{1+(y_\mathrm{min}'(x))^2}{2gy_\mathrm{min}(x)}}\frac{1}{2y_\mathrm{min}(x)}\right)\delta y(x) \\ &=T[y_\mathrm{min}(x)]-\int_0^{x_\mathrm{f}}\mathrm{d}x\left[\partial_x\left(\sqrt{\frac{1+(y_\mathrm{min}'(x))^2}{2gy_\mathrm{min}(x)}}\frac{y_\mathrm{min}'(x)}{1+(y_\mathrm{min}'(x))^2}\right)+\sqrt{\frac{1+(y_\mathrm{min}'(x))^2}{2gy_\mathrm{min}(x)}}\frac{1}{2y_\mathrm{min}(x)}\right]\delta y(x) \quad \left(\text{$\because$ 部分積分}\right) \\ &=T[y_\mathrm{min}(x)]-\int_0^{x_\mathrm{f}}\mathrm{d}x\sqrt{\frac{1+(y_\mathrm{min}'(x))^2}{2gy_\mathrm{min}(x)}}\times\frac{1+(y_\mathrm{min}'(x))^2+2y_\mathrm{min}y_\mathrm{min}''(x)}{2y_\mathrm{min}(x)(1+(y_\mathrm{min}'(x))^2)^2}\delta y(x). \tag{5} \end{align} この第 2 項がどんな微小ずらし $\delta y(x)$ に対しても 0 にならなければならないので, $y_\mathrm{min}(x)$ は $$\boxed{1+(y_\mathrm{min}'(x))^2+2y_\mathrm{min}(x)y_\mathrm{min}''(x)=0, \tag{6}}$$ を満たさなければならない. 実はこの微分方程式の解はサイクロイド (https://ja.wikipedia.org/wiki/%E3%82%B5%E3%82%A4%E3%82%AF%E3%83%AD%E3%82%A4%E3%83%89): $$\begin{cases} x=r_\mathrm{m}(\theta-\sin\theta), \\ y=r_\mathrm{m}(1-\cos\theta), \end{cases}$$ で与えられることが知られている. 実際この時 \begin{align} &\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{\mathrm{d}y/\mathrm{d}\theta}{\mathrm{d}x/\mathrm{d}\theta}=\frac{\sin\theta}{1-\cos\theta}, \\ &\frac{\mathrm{d}^2y}{\mathrm{d}x^2}=\frac{\mathrm{d}}{\mathrm{d}x}\frac{\mathrm{d}y}{\mathrm{d}x}=\left(\frac{\mathrm{d}x}{\mathrm{d}\theta}\right)^{-1}\frac{\mathrm{d}}{\mathrm{d}\theta}\frac{\mathrm{d}y}{\mathrm{d}x}=-\frac{1}{r_\mathrm{m}(1-\cos\theta)^2}, \end{align} であり, これを代入すると (6) 式を満たす.

ちなみに (5) 式第 2 項の $\delta y(x)$ の係数は, 形式的に $T[y(x)]$ の被積分関数 $\sqrt{\frac{1+y'(x)^2}{2gy(x)}}$ を $y(x)$ と $y'(x)$ の関数 $\tau\left(y(x),y'(x)\right)$ とみなせば $$\frac{\partial\tau(y(x),y'(x))}{\partial y(x)}-\partial_x\left(\frac{\partial\tau(y(x),y'(x))}{\partial y'(x)}\right),$$ によって得られる. このように汎函数 $T[y(x)]$ の $y(x)$ を微小にずらすことを変分といい $\delta T/\delta y$ と書く (↔︎ 関数 $f(x)$ の微分 $\mathrm{d}f/\mathrm{d}x$). $T[y(x)]$ を最小化する $y_\mathrm{min}(x)$ は変分 $\delta T/\delta y$ を 0 にする関数として求められる: $$\boxed{\frac{\delta T[y(x)]}{\delta y(x)}=\frac{\partial\tau(y(x),y'(x))}{\partial y(x)}-\partial_x\left(\frac{\partial\tau(y(x),y'(x))}{\partial y'(x)}\right)=0.}$$

§3.2 ラグランジアン¶

汎函数の変分を $0$ にするという条件から微分方程式が得られた. これをニュートン力学に応用できないだろうか. すなわち $$\text{変分が「$ma-F$」となるような汎函数}$$ とはどのようなものだろうか. 実はラグランジアン $L(x,\dot{x})$ なる位置 $x$ と速度 $\dot{x}$ の関数 $$L(x,\dot{x})=\text{(運動エネルギー)}-\text{(位置エネルギー)},$$ を積分した作用 $S[x(t)]$: $$S[x(t)]=\int_{t_\mathrm{i}}^{t_\mathrm{f}}L(x,\dot{x})\mathrm{d}t,$$ がそのような汎函数であることが知られている. すなわち $$\frac{\delta S[x(t)]}{\delta x(t)}=\frac{\partial L}{\partial x}-\partial_t\left(\frac{\partial L}{\partial\dot{x}}\right)=0 \quad \Leftrightarrow \quad F=m\ddot{x}.$$

例 1: 鉛直投げ上げ¶

$$L(y,\dot{y})=\frac{1}{2}m\dot{y}^2-mgy,$$ より $$0=\frac{\delta S[y(t)]}{\delta y(t)}=\frac{\partial L}{\partial y}-\partial_t\left(\frac{\partial L}{\partial\dot{y}}\right)=-mg-\partial_t\left(m\dot{y}\right)=-mg-m\ddot{y}.$$ たしかに鉛直投げ上げの運動方程式 $$m\ddot{y}=-mg,$$ が得られる.

In [194]:
# パラメータ設定
m = 1
g = 9.8
T = 2       # 終了時間
N = 20        # 時間分割数
dt = T / N    # 時間刻み
t = 0:dt:T  # 時間配列
yi = 0
yf = 5

# ラグランジアンの定義
function Lagrangian(y, v)
    return (1/2) * m * v^2 - m * g * y
end

# 作用 S の計算
function action(y::Vector)
    v = diff(y) ./ dt  # 速度の計算（前進差分）
    vi = (y[1] - yi) / dt
    vf = (yf - y[end]) / dt
    S = (Lagrangian(yi,vi) + sum(Lagrangian.(y[1:end-1], v)) + Lagrangian(y[end],vf)) * dt
    return S
end

y0 = [yi + (yf-yi) * k/N for k=1:(N-1)]  # 初期経路 (直線)
result = optimize(action, y0, BFGS())  # BFGS法で最適化
y_opt = result.minimizer

y_EoM(t) = -1/2*g*t*(t-T-2*yf/g/T)  # 解析解

# 結果プロット
plot(t, vcat([yi],y_opt,[yf]), lw=3, label="action", xlabel="t", ylabel="y")
plot!(t, y_EoM, linestyle=:auto, label="EoM")
Out[194]:

例 2: 単振り子¶

No description has been provided for this image

ラグランジアンは $$L=\frac{1}{2}m\dot{x}^2+\frac{1}{2}m\dot{y}^2+mgy.$$ これに $$x=R\sin\theta, \quad y=R\cos\theta,$$ を代入すると $$L(\theta,\dot{\theta})=\frac{1}{2}m(R\dot{\theta}\cos\theta)^2+\frac{1}{2}m(R\dot{\theta}\sin\theta)^2+mgR\cos\theta=\frac{1}{2}mgR^2\dot{\theta}^2+mgR\cos\theta.$$ 運動方程式は $$0=\frac{\delta S[\theta(t)]}{\delta\theta(t)}=\frac{\partial L}{\partial\theta}-\partial_t\left(\frac{\partial L}{\partial\dot{\theta}}\right)=-mgR\sin\theta-\partial_t(mgR^2\dot{\theta})=-mgR\sin\theta-mgR^2\ddot{\theta},$$ すなわち $$R\ddot{\theta}=-g\sin\theta.$$

挑戦問題: 2 重振り子¶

No description has been provided for this image

2 重振り子の運動方程式 $$\begin{cases} \displaystyle \ddot{\theta}_1=\frac{g(C\sin\theta_2-\frac{m_{12}}{m_2}\sin\theta_1)-(l_1v_1^2C+l_2v_2^2)S}{l_1(\frac{m_{12}}{m_2}-C^2)}, \\ \displaystyle \ddot{\theta}_2=\frac{g\frac{m_{12}}{m_2}(C\sin\theta_1-\sin\theta_2)+(\frac{m_{12}}{m_2}l_1v_1^2+l_2v_2^2C)S}{l_2(\frac{m_{12}}{m_2}-C^2)}, \end{cases}$$ を導出できるだろうか. ただし $C=\cos(\theta_1-\theta_2)$, $S=\sin(\theta_1-\theta_2)$, $m_{12}=m_1+m_2$ である.

ラグランジアンは $$L=\frac{1}{2}m_1(\dot{x}_1^2+\dot{y}_1^2)+\frac{1}{2}m_2(\dot{x}_2^2+\dot{y}_2^2)+m_1gy_1+m_2gy_2,$$ それぞれの振り子の位置は $$x_1=l_1\sin\theta_1, \quad y_1=l_1\cos\theta_1,$$ $$x_2=l_1\sin\theta_1+l_2\sin\theta_2, \quad y_2=l_1\cos\theta_1+l_2\cos\theta_2,$$ であり, 最終的にラグランジアンは $\theta_1$, $\theta_2$, $\dot{\theta}_1$, $\dot{\theta}_2$ の関数 $L(\theta_1,\theta_2,\dot{\theta}_1,\dot{\theta}_2)$ である.

§4 量子力学¶

なぜ物体は作用 $S[x(t)]$ を最小にする経路を取るのだろうか. 放たれた瞬間にゴールを知ってるかのようではないか. 実はその疑問は量子力学によって解決される.

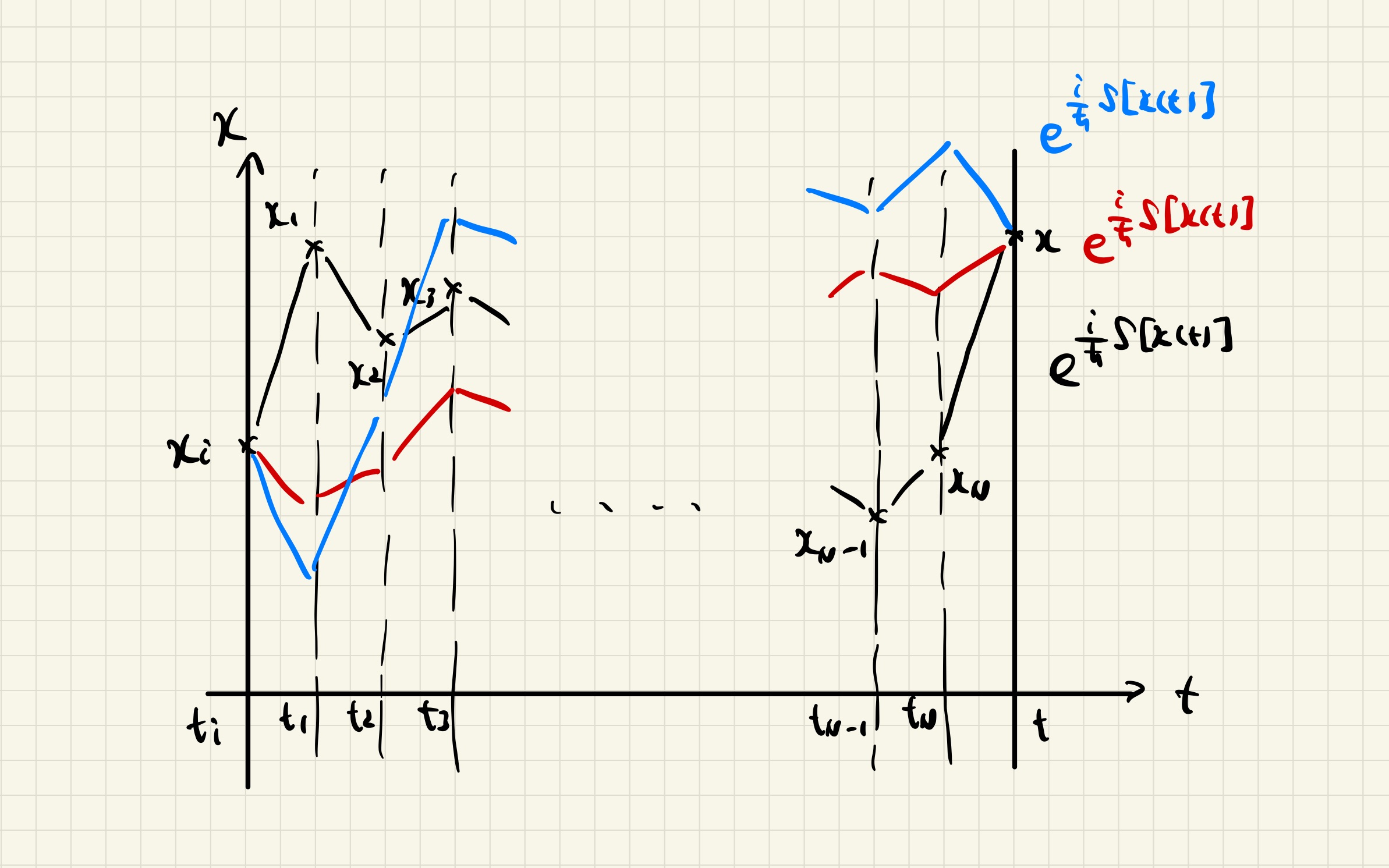No description has been provided for this image 量子力学では粒子は 1 つの経路を通るのではなく, 可能なすべての経路を通り, 各経路 $x(t)$ の効果が $\propto\exp(iS[x(t)]/\hbar)$ で与えられると考える. $\hbar=h/(2\pi)\simeq1.054\times10^{-34}\,\mathrm{J\,s}$ は換算プランク定数である. 初期時刻 $t_\mathrm{i}$ に初期位置 $x_\mathrm{i}$ から初めて, 時刻 $t$ に位置 $x$ に粒子がいる状態に対する波動関数 $\phi(t,x\mid t_\mathrm{i},x_\mathrm{i})$ は次の経路積分で与えられる: $$\phi(t,x\mid t_\mathrm{i},x_\mathrm{i})=\frac{1}{\mathcal{N}}\int\mathcal{D}x\,\exp\left(\frac{i}{\hbar}S[x(t)]\right).$$ 積分の測度は $$\mathcal{D}x=\lim_{\Delta t\to0}\mathrm{d}x_1\mathrm{d}x_2\cdots\mathrm{d}x_N,$$ であり, 定数 $\mathcal{N}$ は全確率が $1$ になるように定義される. 波動関数 $\phi(t,x\mid t_\mathrm{i},x_\mathrm{i})$ をもって, 時刻 $t$ に位置 $x$ で粒子が観測される確率は $P(t,x\mid t_\mathrm{i},x_\mathrm{i})=\left|\phi(t,x\mid t_\mathrm{i},x_\mathrm{i})\right|^2$ で与えられる.

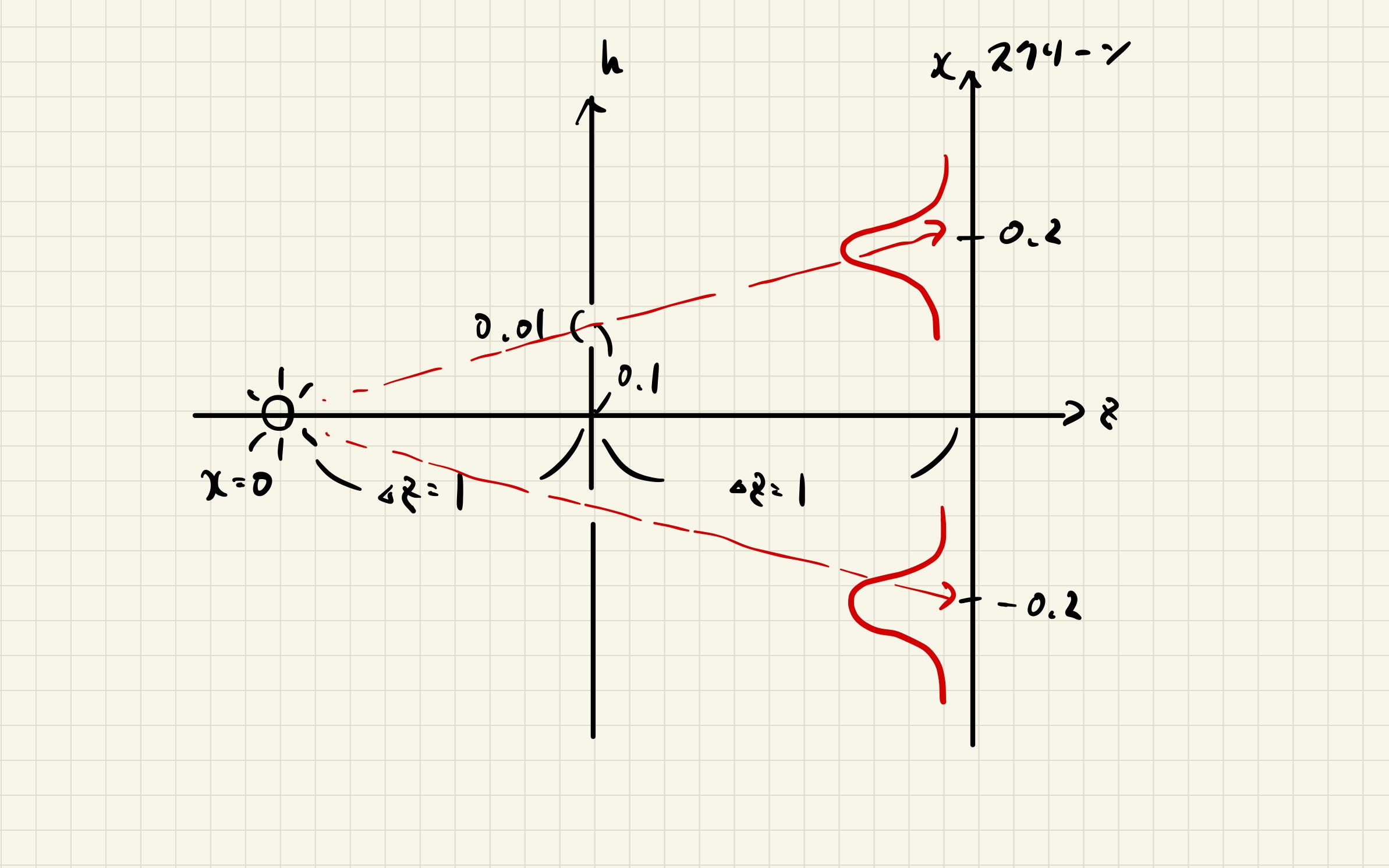作用 $S[x(t)]$ の典型的な値に対し $\hbar$ が非常に小さいような「古典的」な系を考えてみよう. この場合 $S[x(t)]$ がわずかに変わるだけで複素数 $\exp(iS[x(t)]/\hbar)$ は激しく振動し, 近い経路同士の効果が打ち消し合うことになる. 結局, 近い経路で作用がほとんど変化しない ($\delta S/\delta x=0$) 「古典経路」が互いに打ち消し合わず, 選択されやすいというだけのことである. $\hbar$ が小さくない系においては, より多様な経路の効果が効いてきて「量子力学的」振る舞いを見ることができる. 実験してみよう. No description has been provided for this image 時刻 $t=0$ に位置 $z=0$ から電子を 1 個発射して, 時刻 $t=2$ に位置 $z=2$ にあるスクリーンに当てることを考える. 位置 $z=1$ には 2 つスリットの空いた壁があり, 電子はスリットしか通過できない. スリット位置は $0.99\leq h\leq 1.01$ と $-1.01\leq h\leq-0.99$ である. 簡単のため時刻 $t=1$ に位置 $h$ を通過し時刻 $t=2$ にスクリーン位置 $x$ にあたる, 途中は直線の経路のみを考える. すなわち作用は $h$ と $x$ のみの関数として $$S(h,x) = \frac{1}{2}m\left[\left(\frac{\Delta z}{\Delta t}\right)^2+\left(\frac{h}{\Delta t}\right)^2\right]\Delta t+\frac{1}{2}m\left[\left(\frac{\Delta z}{\Delta t}\right)^2+\left(\frac{x-h}{\Delta t}\right)^2\right]\Delta t,$$ で与えられる. $\Delta z=\Delta t=1$ である. スリット 1 ($0.99\leq h\leq1.01$) を通った寄与は $$\phi_1(x)=\int_{0.99}^{1.01}\mathrm{d}h\,\exp\left(\frac{i}{\hbar}S(h,x)\right),$$ で与えられるし, スリット 2 ($-1.01\leq h\leq-0.99$) を通った寄与は $$\phi_2(x)=\int_{-1.01}^{-0.99}\mathrm{d}h\,\exp\left(\frac{i}{\hbar}S(h,x)\right),$$ 全寄与は $$\phi(x)=\phi_1(x)+\phi_2(x),$$ となる. 簡単のため規格化定数 $\mathcal{N}$ は無視した.

In [196]:
slit = 0.1
width = 0.01
dz = 1
dt = 1
m = 1
Out[196]:
1
In [198]:
function actionS(h,x)
    return 1/2*m*((dz/dt)^2+(h/dt)^2)*dt + 1/2*m*((dz/dt)^2+((x-h)/dt)^2)*dt
end

function Phi_slit1(x,hbar)
    return quadgk(h -> exp(im/hbar*actionS(h,x)), slit-width/2, slit+width/2)[1]
end

function Phi_slit2(x,hbar)
    return quadgk(h -> exp(im/hbar*actionS(h,x)), -slit-width/2, -slit+width/2)[1]
end

function Phi_tot(x,hbar)
    return Phi_slit1(x,hbar) + Phi_slit2(x,hbar)
end
Out[198]:
Phi_tot (generic function with 1 method)
In [200]:
lnhbar = -5
plot(-0.4:0.001:0.4, x->norm(Phi_slit1(x,10.0^lnhbar))^2, title=@sprintf("hbar=1e%d",lnhbar))
plot!(-0.4:0.001:0.4, x->norm(Phi_slit2(x,10.0^lnhbar))^2)
Out[200]:
In [204]:
lnhbar = -5
plot(-0.4:0.001:0.4, x->norm(Phi_tot(x,10.0^lnhbar))^2, title=@sprintf("hbar=1e%d",lnhbar))
Out[204]:
In [206]:
lnhbar = -4
plot(-0.4:0.001:0.4, x->norm(Phi_slit1(x,10.0^lnhbar))^2, title=@sprintf("hbar=1e%d",lnhbar))
plot!(-0.4:0.001:0.4, x->norm(Phi_slit2(x,10.0^lnhbar))^2)
Out[206]:
In [208]:
lnhbar = -4
plot(-0.4:0.001:0.4, x->norm(Phi_tot(x,10.0^lnhbar))^2, title=@sprintf("hbar=1e%d",lnhbar))
Out[208]:
In [210]:
lnhbar = -3
plot(-0.4:0.001:0.4, x->norm(Phi_slit1(x,10.0^lnhbar))^2, title=@sprintf("hbar=1e%d",lnhbar))
plot!(-0.4:0.001:0.4, x->norm(Phi_slit2(x,10.0^lnhbar))^2)
Out[210]:
In [212]:
lnhbar = -3
plot(-0.4:0.001:0.4, x->norm(Phi_tot(x,10.0^lnhbar))^2, title=@sprintf("hbar=1e%d",lnhbar))
Out[212]:
In [214]:
lnhbar = -2
plot(-0.4:0.001:0.4, x->norm(Phi_slit1(x,10.0^lnhbar))^2, title=@sprintf("hbar=1e%d",lnhbar))
plot!(-0.4:0.001:0.4, x->norm(Phi_slit2(x,10.0^lnhbar))^2)
Out[214]:
In [216]:
lnhbar = -2
plot(-0.4:0.001:0.4, x->norm(Phi_tot(x,10.0^lnhbar))^2, title=@sprintf("hbar=1e%d",lnhbar))
Out[216]:

最終課題¶

ニュートン力学・解析力学・量子力学のいずれかで好きなシミュレーションを実装せよ.